full explanantion of Thermodynamic laws

The zeroth law of thermodynamics

The zeroth law of thermodynamics defines thermal equilibrium and forms a basis for the definition of temperature: If two systems are each in thermal equilibrium with a third system, then they are in thermal equilibrium with each other.

The zeroth law of thermodynamics provides for the foundation of temperature as an empirical parameter in thermodynamic systems and establishes the transitive relation between the temperatures of multiple bodies in thermal equilibrium. The law may be stated in the following form:

If two systems are both in thermal equilibrium with a third system, then they are in thermal equilibrium with each other.

Though this version of the law is one of the most commonly stated versions, it is only one of a diversity of statements that are labelled as "the zeroth law". Some statements go further, so as to supply the important physical fact that temperature is one-dimensional and that one can conceptually arrange bodies in a real number sequence from colder to hotter.

These concepts of temperature and of thermal equilibrium are fundamental to thermodynamics and were clearly stated in the nineteenth century. The name 'zeroth law' was invented by Ralph H. Fowler in the 1930s, long after the first, second, and third laws were widely recognized. The law allows the definition of temperature in a non-circular way without reference to entropy, its conjugate variable. Such a temperature definition is said to be 'empirical'.

The first law of thermodynamics

" The first law of thermodynamics states that, when energy passes into or out of a system (as work, heat, or matter), the system's internal energy changes in accord with the law of conservation of energy."

The first law of thermodynamics is a version of the law of conservation of energy, adapted for thermodynamic processes. In general, the conservation law states that the total energy of an isolated system is constant; energy can be transformed from one form to another but can be neither created nor destroyed.

In a closed system (i.e. there is no transfer of matter into or out of the system), the first law states that the change in internal energy of the system (ΔU_system) is equal to the difference between the heat supplied to the system (Q) and the work (W) done by the system on its surroundings. (Note, an alternate sign convention, not used in this article, is to define W as the work done on the system by its surroundings):

${\displaystyle \Delta U_{\rm {system}}=Q-W}$.

For processes that include the transfer of matter, a further statement is needed.

When two initially isolated systems are combined into a new system, then the total internal energy of the new system, U_system, will be equal to the sum of the internal energies of the two initial systems, U₁ and U₂:

${\displaystyle U_{\rm {system}}=U_{1}+U_{2}}$.

The First Law encompasses several principles:

• The Conservation of energy, which says that energy can be neither created nor destroyed, but can only change form. A particular consequence of this is that the total energy of an isolated system does not change.

• The concept of internal energy and its relationship to temperature. If a system has a definite temperature, then its total energy has three distinguishable components, termed kinetic energy (energy due to the motion of the system as a whole), potential energy (energy resulting from an externally imposed force field), and internal energy. The establishment of the concept of internal energy distinguishes the first law of thermodynamics from the more general law of conservation of energy.

${\displaystyle E_{\rm {total}}=\mathrm {KE} _{\rm {system}}+\mathrm {PE} _{\rm {system}}+U_{\rm {system}}}$

What is WORK ?

• Work is a process of transferring energy to or from a system in ways that can be described by macroscopic mechanical forces acting between the system and its surroundings. The work done by the system can come from its overall kinetic energy, from its overall potential energy, or from its internal energy.

For example, when a machine (not a part of the system) lifts a system upwards, some energy is transferred from the machine to the system. The system's energy increases as work is done on the system and in this particular case, the energy increase of the system is manifested as an increase in the system's gravitational potential energy. Work added to the system increases the potential energy of the system:

• When matter is transferred into a system, that masses' associated internal energy and potential energy are transferred with it.

${\displaystyle \left(u\,\Delta M\right)_{\rm {in}}=\Delta U_{\rm {system}}}$

where u denotes the internal energy per unit mass of the transferred matter, as measured while in the surroundings; and ΔM denotes the amount of transferred mass.

• The flow of heat is a form of energy transfer. Heating is the natural process of moving energy to or from a system other than by work or the transfer of matter. In an isolated system, the internal energy can only be changed by the transfer of energy as heat:

${\displaystyle \Delta U_{\rm {system}}=Q}$

Combining these principles leads to one traditional statement of the first law of thermodynamics: it is not possible to construct a machine that will perpetually output work without an equal amount of energy input to that machine. Or more briefly, a perpetual motion machine of the first kind is impossible.

The second law of thermodynamics

"The second law of thermodynamics states that in a natural thermodynamic process, the sum of the entropies of the interacting thermodynamic systems never decreases. Another form of the statement is that heat does not spontaneously pass from a colder body to a warmer body."

The second law of thermodynamics indicates the irreversibility of natural processes, and, in many cases, the tendency of natural processes to lead towards spatial homogeneity of matter and energy, and especially of temperature. It can be formulated in a variety of interesting and important ways. One of the simplest is the Clausius statement, that heat does not spontaneously pass from a colder to a hotter body.

It implies the existence of a quantity called the entropy of a thermodynamic system. In terms of this quantity, it implies that

When two initially isolated systems in separate but nearby regions of space, each in thermodynamic equilibrium with itself but not necessarily with each other, are then allowed to interact, they will eventually reach a mutual thermodynamic equilibrium. The sum of the entropies of the initially isolated systems is less than or equal to the total entropy of the final combination. Equality occurs just when the two original systems have all their respective intensive variables (temperature, pressure) equal; then the final system also has the same values.

The second law is applicable to a wide variety of processes, both reversible and irreversible. According to the second law, in a reversible heat transfer, an element of heat transferred, δQ, is the product of the temperature (T), both of the system and of the sources or destination of the heat, with the increment (dS) of the system's conjugate variable, its entropy (S):

${\displaystyle \delta Q=T\,dS\,.}$

While reversible processes are a useful and convenient theoretical limiting case, all-natural processes are irreversible. A prime example of this irreversibility is the transfer of heat by conduction or radiation. It was known long before the discovery of the notion of entropy that when two bodies, initially of different temperatures, come into direct thermal connection, then heat immediately and spontaneously flows from the hotter body to the colder one.

Entropy may also be viewed as a physical measure concerning the microscopic details of the motion and configuration of a system when only the macroscopic states are known. Such details are often referred to as disorder on a microscopic or molecular scale, and less often as the dispersal of energy. For two given macroscopically specified states of a system, there is a mathematically defined quantity called the 'difference of information entropy between them'. This defines how much additional microscopic physical information is needed to specify one of the macroscopically specified states, given the macroscopic specification of the other – often a conveniently chosen reference state which may be presupposed to exist rather than explicitly stated. A final condition of a natural process always contains microscopically specifiable effects which are not fully and exactly predictable from the macroscopic specification of the initial condition of the process. This is why entropy increases in natural processes – the increase tells how much extra microscopic information is needed to distinguish the initial macroscopically specified state from the final macroscopically specified state. Equivalently, in a thermodynamic process, energy spreads.

The third law of thermodynamics

"The third law of thermodynamics states that a system's entropy approaches a constant value as the temperature approaches absolute zero. With the exception of non-crystalline solids (glasses), the entropy of a system at absolute zero is typically close to zero."

The third law of thermodynamics can be stated as:

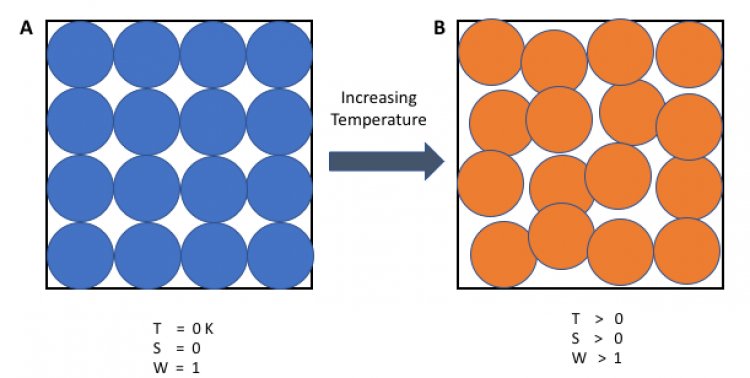
A system's entropy approaches a constant value as its temperature approaches absolute zero.

At zero temperature, the system must be in the state with the minimum thermal energy, the ground state. The constant value (not necessarily zero) of entropy at this point is called the residual entropy of the system. Note that, with the exception of non-crystalline solids (e.g. glasses) the residual entropy of a system is typically close to zero. However, it reaches zero only when the system has a unique ground state (i.e. the state with the minimum thermal energy has only one configuration, or microstate). Microstates are used here to describe the probability of a system being in a specific state, as each microstate is assumed to have the same probability of occurring, so macroscopic states with fewer microstates are less probable. In general, entropy is related to the number of possible microstates according to the Boltzmann principle:

${\displaystyle S=k_{\mathrm {B} }\,\mathrm {ln} \,\Omega }$

Where S is the entropy of the system, k_B Boltzmann's constant, and Ω the number of microstates. At absolute zero there is only 1 microstate possible (Ω=1 as all the atoms are identical for a pure substance and as a result all orders are identical as there is only one combination) and ln(1) = 0.